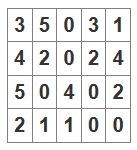
В этот раз задача звучит так. Имеем представление городских кварталов виде матрицы. Число в каждой клетке — это число пассажиров, которые хотят уехать (в каждом квартале только одна остановка). Автобус начинает двигаться в верхнем левом углу и заканчивает в правом. Он может двигаться только вправо или вниз. Нужно проложить маршрут так, чтобы автобус подобрал максимальное число пассажиров.
Автобус начинает двигаться в левом верхнем углу, поэтому сначала он подберет 3 пассажира из соответствующего квартала. Теперь надо решать: двигаемся вниз или вправо. Надо рассмотреть все возможные варианты и выбрать наилучший. И сделать это за один обход матрицы!
Введем в рассмотрение еще одну матрицу maxPassengers такой же размерности, как исходная. В левом верхнем углу у нее будет число 3, как и у исходной. Теперь используем условие о том, что перемещение может быть только вправо или вниз. Это означает, что в клетки в верней строке можно попасть только движением влево из соседней клетки в этой же строке.
maxPassengers[0][0] = map[0][0]; for (int c = 1; c < numColumns; c++) { maxPassengers[0][c] = map[0][c] + maxPassengers[0][c - 1]; } |
Аналогично, в клетки крайнего левого столбца можно попасть только движением вниз из верхней клетки:
for (int r = 1; r < numRows; r++) { maxPassengers[r][0] = map[r][0] + maxPassengers[r - 1][0]; } |
Это были два частных случая. Теперь рассмотрим общий случай заполнения клеток матрицы maxPassengers. Мы знаем, что в каждую клетку можно попасть сверху или слева. Поэтому вычисляем значение в этой клетке так: к максимуму из значений в клетках сверху и слева прибавляем число пассажиров в самой клетке:
for (int r = 1; r < numRows; r++) { for (int c = 1; c < numColumns; c++) { maxPassengers[r][c] = map[r][c] + Math.max(maxPassengers[r - 1][c], maxPassengers[r][c - 1]); } } |
Теперь скомпонуем фрагменты и запустим программу:
public static int maxPassengerPickup(int[][] map) {
int numRows = map.length;
if (numRows == 0) return 0;
int numColumns = map[0].length;
String[][] directions = new String[numRows][numColumns];
int[][] maxPassengers = new int[numRows][numColumns];
maxPassengers[0][0] = map[0][0];
directions[0][0] = "start here";
for (int c = 1; c < numColumns; c++) {
maxPassengers[0][c] = map[0][c] + maxPassengers[0][c - 1];
directions[0][c] = "from left";
}
for (int r = 1; r < numRows; r++) {
maxPassengers[r][0] = map[r][0] + maxPassengers[r - 1][0];
directions[r][0] = "from above";
}
for (int r = 1; r < numRows; r++) {
for (int c = 1; c < numColumns; c++) {
int max = -1;
if (maxPassengers[r - 1][c] > maxPassengers[r][c - 1]) {
max = maxPassengers[r - 1][c];
directions[r][c] = "from above";
} else {
max = maxPassengers[r][c - 1];
directions[r][c] = "from left";
}
maxPassengers[r][c] = map[r][c] + max;
}
}
for (int r = 0; r < numRows; r++) {
for (int c = 0; c < numColumns; c++) {
System.out.print(directions[r][c] + " ");
}
System.out.println("");
}
return maxPassengers[numRows - 1][numColumns - 1];
}
// для метода main()
int blocks[][] = {{3, 5, 0, 3, 1},
{4, 2, 0, 2, 4},
{5, 0, 4, 0, 2},
{2, 1, 1, 0, 0}
};
int max = maxPassengerPickup(blocks);
System.out.println(max); |
Получим такой результат — будет подобрано 19 человек по такому маршруту:
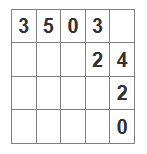
У меня для визуализации использована вспомогательная матрица directions — для каждой клетки указано, из какой соседней для нее был максимум: from above (лишний пробел для выравниваний) — из верхней, from left — из левой. Итого:
start here from left from left from left from left from above from above from left from above from left from above from left from left from left from above from above from left from above from left from above |
Начинаем смотреть с правой нижней и получаем тот маршрут, который я уже привел.
За основу взята статья: оригинал

 17 февраля, 2018
17 февраля, 2018  rius
rius  Posted in
Posted in  Tags:
Tags: