10 ноября, 2015 
rius 
Когда я посмотрел видео Маттиаса Ванделя видео о трех-позиционном соединении, я сразу решил, что попробую сделать макет. Однако, у меня нет в распоряжении лобзика. И заказывать с ходу 3d печать тоже лениво (3d модель доступна тут 3d модель ). В результате я решил сделать макет из картона.
При вдумчивом просмотре можно заметить, что каждая из двух стыкуемых деталей состоит из треугольной пирамиды, бруска и 3 одинаковых зубцов. Вот с этим-то зубцом и было больше всего работы. Для подготовки развертки зубца пришлось вспоминать школьный курс тригонометрии. Несмотря на кажущуюся сложность в нем есть ряд закономерностей, который облегчает жизнь: в сечении двух плоскостей лежит равносторонний треугольник, сами плоскости сечения параллельны, одна из сторон делится зубцом пополам, еще одна сторона делится на три равные части и т.д.
Развертка зубца. Отрезки одинаковой длины отмечены одинаковыми цветами. Длина красных отрезков равна половине длины ребра куба. В случае необходимости увеличивайте размер клапанов.
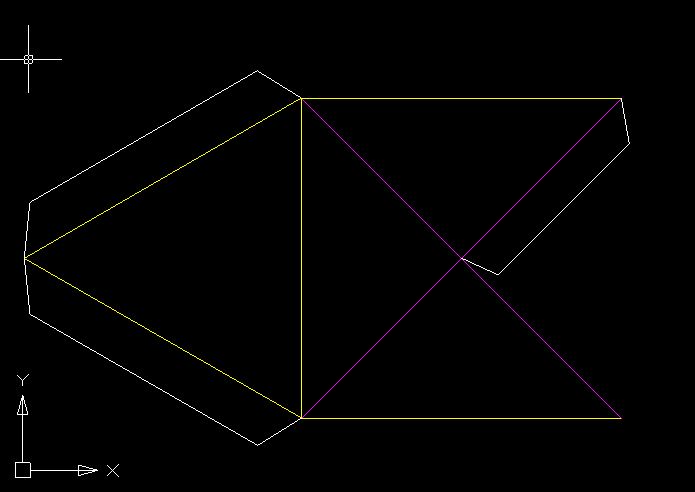
Развертка пирамиды.
Заранее прошу прощения за мелкие огрехи в чертеже — я не ставил задачи выдержать абсолютную точность, т. к. при сгибании картона/ватмана (да даже просто бумаги) будет набегать бОльшая погрешность. В качестве материала я выбрал ватман — он обеспечивает некоторую жесткость элементов.
Скачать чертеж: скачать
Итак, из чертежа вам понадобится:
— 6 зубцов
— 2 пирамидки
— 2 параллелепипеда
В принципе пирамиды и параллелепипеды можно объединить, придется меньше клеить.
Для соединения элементов я сначала попробовал суперклей. Но быстро испачкал в нем пальцы, когда прижимал склеиваемые элементы из ватмана. Поэтому в конечном итоге выбор пал на комбинацию двустороннего скотча и обычного скотча.
Готовые изделия, запасной зубец и спичечный коробок для масштаба.
Для моих задач прекрасно подошло.
Posted in